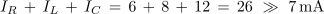|
|
| Vrstica 16: |
Vrstica 16: |
| | | | |
| | Aritmetična vsota efektivnih tokov je v danem primeru precej večja od efektivnega toka izvora. Nekaj podobnega smo ugotovili tudi pri zaporedni vezavi vseh treh elementov v poskusu 3.2.2, le da smo takrat imeli opravka z napetostmi. | | Aritmetična vsota efektivnih tokov je v danem primeru precej večja od efektivnega toka izvora. Nekaj podobnega smo ugotovili tudi pri zaporedni vezavi vseh treh elementov v poskusu 3.2.2, le da smo takrat imeli opravka z napetostmi. |
| - |
| |
| - |
| |
| - |
| |
| - | == Kazalčni diagram napetosti in tokov ==
| |
| - | [[Image:eele_slika_3_2_14.svg|thumb|right|Slika 3.2.14: Kazalčni diagram vzporednega RLC kroga]]
| |
| - | [[Image:eele_slika_3_2_15.svg|thumb|right|Slika 3.2.15: Kazalčni diagrami vzporednega izmeničnega kroga]]
| |
| - |
| |
| - | Skupna količina elementom kroga je napetost ''U'', na že znani način pa dobimo kazalčni diagram, ki ga prikazuje sl.3.2.14:
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *V vzporednem izmeničnem krogu z uporom, tuljavo in kondenzatorjem sta kazalca tokov tuljave in kondenzatorja '''nasprotno usmerjena''' in '''pravokotna''' na kazalec toka skozi upor.
| |
| - | *Toka tuljave in kondenzatorja sta v '''protifazi'''.
| |
| - | *Efektivni tok izvora je enak '''geometrični vsoti''' efektivnih tokov upora, tuljave in kondenzatorja.
| |
| - | </pomembno>
| |
| - |
| |
| - |
| |
| - | Razmerje tokov tuljave in kondenzatorja je odvisno od razmerja induktivne in kapacitivne upornosti. Možni so trije splošni primeri:
| |
| - |
| |
| - |
| |
| - | <latex>{I_L} \,\,\textgreater \,\, {I_C}\,;\,\,\,\,\,{I_L}\, = \,{I_C}\,\,\,\,\,{\rm{ali}}\,\,\,\,\,{I_L}\,\, \textless \,\,{I_C}</latex>
| |
| - |
| |
| - |
| |
| - | Kazalčne diagrame za navedene tri primere kaže primerjalno slika 3.2.15 a, b in c.
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *V izmeničnem krogu z vzporedno vezavo upora, tuljave in kondenzatorja tok lahko '''prehiteva''', '''zaostaja''' ali pa je v '''fazi''' z napetostjo izvora (podobno kot pri zaporedni vezavi istih elementov).
| |
| - | *Vzporedna vezava upora, tuljave in kondenzatorja ima lahko značaj in lastnosti vzporedne vezave '''upora''' in '''tuljave''' ali '''upora''' in '''kondenzatorja''' ali samo '''upora'''.
| |
| - | </pomembno>
| |
| - |
| |
| - |
| |
| - | Vzporedna vezava upora, tuljave in kondenzatorja povzroča v izmeničnem krogu fazni kot med - 90 º in + 90 º.
| |
| - |
| |
| - |
| |
| - | <latex> - 90^{\,\circ} \,\, \textless\,\, \varphi \,\, \textless \,\, + 90^{\,\circ} </latex>
| |
| - |
| |
| - |
| |
| - |
| |
| - | == Trikotnik tokov in prevodnosti ==
| |
| - | [[Image:eele_slika_3_2_16.svg|thumb|right|Slika 3.2.16: Trikotnik tokov in prevodnosti vzporedne vezave upora, tuljave in kondenzatorja]]
| |
| - |
| |
| - | Iz kazalčnega diagrama na sl. 3.2.15 izrišemo '''trikotnik tokov''' (sl. 3.2.16 a), z deljenjem njegovih stranic s skupno količino elementov '''''U''''' pa dobimo trikotnik prevodnosti vezave (sl. 3.2.16 b).
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Toki in prevodnosti izmeničnega kroga z vzporedno vezavo upora, tuljave in kondenzatorja tvorijo '''pravokotna trikotnika'''.
| |
| - | *Toke in prevodnosti vzporedne vezave upora, tuljave in kondenzatorja seštevamo '''geometrično'''.
| |
| - | </pomembno>
| |
| - |
| |
| - |
| |
| - | Po pravilih za računanje v pravokotnem trikotniku lahko zapišemo:
| |
| - |
| |
| - |
| |
| - | <latex>I\, = \,\sqrt {{I_R}^2\, +\, {{\left( {{I_L} \,- \,{I_C}} \right)}^2}} \,;\,\,\,\,\,Y \,=\, \sqrt {{G^2}\, +\, {{\left( {{B_L}\, -\, {B_C}} \right)}^2}}\,\,\, ...</latex>
| |
| - |
| |
| - | ali tudi
| |
| - |
| |
| - | <latex>\cos \varphi \, =\, \frac{I_R}{I}\, =\, \frac{G}{Y}\,;\,\,\,\,\,{\rm{tg}}\,\varphi \, =\, \frac{{I_L}\, - \,{I_C}}{I_R}\, =\, \frac{{B_L}\, -\, {B_C}}{G}\,\,\,...,</latex>
| |
| - |
| |
| - |
| |
| - | kar pri treh znanih količinah trikotnika omogoča računanje četrte količine.
| |
| - | V medsebojnem odnosu kapacitivne in induktivne prevodnosti in posledično tudi tokov vzporedne vezave elementov (sl. 3.2.15) obstajajo tri možnosti:
| |
| - |
| |
| - |
| |
| - | <latex>{B_C}\,\, \textgreater\,\, {B_L}\,;\,\,\,\,\,{B_C}\,\, \textless\,\, {B_L}\,\,\,\,\,{\rm{in}}\,\,\,\,\,{B_C}\, =\, {B_L}.</latex>
| |
| - |
| |
| - |
| |
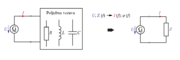
| - | V vseh treh primerih admitanco vezave izračunamo na enak, zgoraj navedeni način. Zanimiv primer nastopi v primeru enakosti:
| |
| - |
| |
| - |
| |
| - | <latex>{B_L}\, = \,{B_C}\,\,\,\,\, \Rightarrow\,\,\,\,\, {B_L}\, - \,{B_C}\, =\, 0</latex>
| |
| - |
| |
| - | <latex>Y\, = \,\sqrt {{G^2}\, +\, {{\left( {{B_L} \,- \,{B_C}} \right)}^2}} \, = \,G</latex>
| |
| - |
| |
| - | <latex>\tan \varphi \, =\, \frac{{B_L}\, -\, {B_C}}{G}\, =\, 0 \,\,\,\,\,\Rightarrow \,\,\,\,\,\varphi \, =\, 0</latex>
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Admitanca vzporedne vezave upora, tuljave in kondenzatorja je v primeru '''enakosti''' njunih '''jalovih''' prevodnosti '''najmanjša'''. Enaka je le '''delovni''' prevodnosti in '''ne povzroča faznega premika''' med napetostjo in tokom izvora.</pomembno>
| |
| - |
| |
| - |
| |
| - | V primeru enakosti induktivne in kapacitivne prevodnosti ima vzporedni vezava upora, tuljave in kondenzatorja, podobno kot zaporedna vezava, še druge zanimive lastnosti, ki pa jih bomo obravnavali pri resonančnih pojavih.
| |
| - |
| |
| - |
| |
| - | '''Primera:'''
| |
| - | <primer>
| |
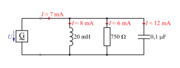
| - | 1. Vzporedna vezava upora z upornostjo 750 Ω, tuljave z induktivnostjo 20 mH in kondenzatorja s kapacitivnostjo 100 nF je priključena na izvor sinusne napetosti frekvence 5 kHz. Izračunaj admitanco, impedanco ter fazni kot, ki ga vezava povzroča v električnem krogu.|||
| |
| - | <latex>G \,=\, \frac{1}{R} \,= \,\frac{1}{750} \,=\, {\rm{1,33\,mS}}</latex>
| |
| - |
| |
| - | <latex>{B_L}\, =\, \frac{1}{2\pi fL} \,= \,\frac{1}{2\pi \, \cdot \,5 \,\cdot \,{{10}^3} \,\cdot\, 20 \,\cdot\, {{10}^{ - 3}}}\, = \,{\rm{1,6\,mS}}</latex>
| |
| - |
| |
| - | <latex>{B_C}\, =\, 2\pi fC \,=\, 2\pi \, \cdot \,5\, \cdot \,{10^3} \,\cdot \,100 \,\cdot \,{10^{-9}}\, =\,{\rm{3,14\,mS}}</latex>
| |
| - |
| |
| - | <latex>Y \,= \,\sqrt {{{{\rm{1,33}}}^2} \,+\, {{\left( {{\rm{1,6}} \,-\, {\rm{3,14}}} \right)}^2}} \, =\, {\rm{2,03\,mS}}</latex>
| |
| - |
| |
| - | <latex>Z\, =\, \frac{1}{Y} \,=\, \frac{1}{{\rm{2,03}} \,\cdot\, {{10}^{ - 3}}}\, =\, 492\,\Omega </latex>
| |
| - |
| |
| - | <latex>\tan \varphi \, =\, \frac{{B_L} \,- \,{B_C}}{G}\, = \,\frac{{\rm{1,6}}\, - \,{\rm{3,14}}}{{\rm{1,33}}} \,=\, {\rm{- 1,157}}\,\,\,\,\, \Rightarrow \,\,\,\,\,\varphi \, = \, {\rm{- 49,2}}^{\,\circ} </latex>
| |
| - | </primer>
| |
| - |
| |
| - | <primer>
| |
| - | 2. Izračunaj kapacitivnost kondenzatorja, ki ga moramo vezati vzporedno z vzporedno vezanima uporom z upornostjo 2,7 kΩ in tuljavo z induktivnostjo 200 μH, če želimo, da bo vezava pri krožni frekvenci 2,5 • 10<sup>6</sup> s<sup>-1</sup> povzročala zaostajanje toka za napetostjo za 30 º.|||
| |
| - | <latex>G \,= \,\frac{1}{R}\, =\, \frac{1}{2700} \,=\, {\rm{0,37\,mS}}</latex>
| |
| - |
| |
| - | <latex>{B_L}\, =\, \frac{1}{\omega L}\, =\, \frac{1}{{\rm{2,5}} \,\cdot \,{{10}^6} \,\cdot \,200\, \cdot \,{{10}^{-6}}}\, =\, 2{\rm{\,mS}}</latex>
| |
| - |
| |
| - | <latex>\tan \varphi \, = \,\frac{{B_L}\, - \,{B_C}}{G}\,\,\,\,\, \Rightarrow\,\,\,\,\, {B_L} \,- \,{B_C}\, = \,G \,\cdot \,\tan \varphi \, =\, {\rm{0,37}} \,\cdot \,{10^{-3}} \,\cdot \,\tan 30^{\,\circ}\, =\,{\rm{0,214\,mS}}</latex>
| |
| - |
| |
| - | <latex>{B_C}\, = \,{B_L}\, -\, {\rm{0,214\,mS}} \,= \,2\, -\, {\rm{0,214}}\, =\, {\rm{1,79\,mS}}</latex>
| |
| - |
| |
| - | <latex>{B_C}\, =\, \omega C \,\,\,\,\,\Rightarrow\,\,\,\,\, C \,= \,\frac{B_C}{\omega } \,= \,\frac{{\rm{1,79}} \,\cdot \,{{10}^{-3}}}{{\rm{2,5}}\, \cdot \,{{10}^6}}\, =\, 714{\rm{\,pF}}</latex>
| |
| - | </primer>
| |
| | | | |
| | | | |
| | {{Hierarchy footer}} | | {{Hierarchy footer}} |
![](javascript: loadPicture("Eele_slika_3_2_13.svg", 886);)
![](javascript: loadPicture("Eele_slika_3_2_2.svg", 1248);)
3.2.3.2 Trikotnik tokov in prevodnosti
