Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| Vrstica 6: | Vrstica 6: | ||
| - | Sestavljeno breme naj | + | Sestavljeno breme naj bo priključeno na tokovni vir, ki mu pripada kazalec <latex>{\underline I}</latex>. Kazalcu napetosti <latex>{\underline U}</latex> sestavljenega bremena ustreza produkt <latex>{\underline Z}{\underline I}</latex>; od tu sledita kazalca preostalih tokov in kazalca napetosti prvih dveh bremen: |
| Vrstica 12: | Vrstica 12: | ||
| - | Iz preprostega primera je razvidno, da je način dela enak kot pri enosmernih uporovnih vezjih | + | Iz preprostega primera je razvidno, da je način dela enak kot pri enosmernih uporovnih vezjih. Tamkajšnje realne enačbe zamenjujejo tokrat kompleksne; potrebna računska opravila so zaradi tega ustrezno daljša. V ilustracijo naj bo naslednji zgled. |
| - | '''Zgled 4 | + | '''Zgled 4 ''' |
| - | Impedance bremen v vezju so: <latex>{\underline Z _1} = (1 - {\rm{j}})\,{\rm{\Omega }}</latex>, <latex>{\underline Z _2} = 2{\rm{j}}\,{\rm{\Omega }}</latex> in <latex>{\underline Z _3} = 2\,{\rm{\Omega }}</latex>; prvo breme ima delno kapacitivni značaj, drugo čisto induktivni, tretje pa ima čisto uporovni značaj. Tok <latex>i</latex> vira naj določa kazalec <latex>{\underline I} = 2{\rm{j}}\,{\rm{A }}</latex>. Izračunajmo kazalce napetosti in tokov | + | Impedance bremen v vezju so: <latex>{\underline Z _1} = (1 - {\rm{j}})\,{\rm{\Omega }}</latex>, <latex>{\underline Z _2} = 2{\rm{j}}\,{\rm{\Omega }}</latex> in <latex>{\underline Z _3} = 2\,{\rm{\Omega }}</latex>; prvo breme ima delno kapacitivni značaj, drugo čisto induktivni, tretje pa ima čisto uporovni značaj. Tok <latex>i</latex> vira naj določa kazalec <latex>{\underline I} = 2{\rm{j}}\,{\rm{A }}</latex>. Izračunajmo kazalce napetosti in tokov. ⇒ Sledimo zgoraj nakazanim korakom: |
Redakcija: 21:49, 7. junij 2010
Slika:OET2 a poglavje 27 slika 15.svg
Sestavljena vezave treh kompleksnih bremen.
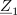
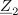
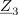
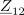
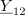
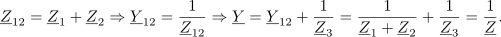
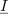
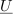
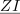
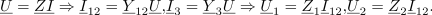
Iz preprostega primera je razvidno, da je način dela enak kot pri enosmernih uporovnih vezjih. Tamkajšnje realne enačbe zamenjujejo tokrat kompleksne; potrebna računska opravila so zaradi tega ustrezno daljša. V ilustracijo naj bo naslednji zgled.
Zgled 4
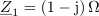
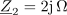
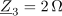
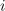
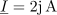
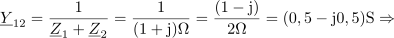
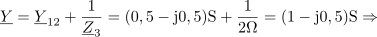
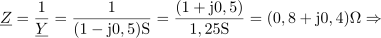
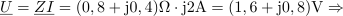
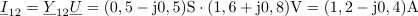
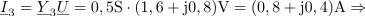
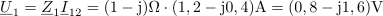
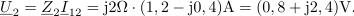
Podpoglavja:
| | 2.4.1 Realna in imaginarna dela imitanc |
