3.2.2 Zaporedna vezava upora, tuljave in kondenzatorja

Iz e-ELEKTROTEHNIKA plus

(Primerjava redakcij)

Redakcija: 13:12, 21. december 2009

Poskus 3.2.2:

Zaporedno vezavo upora z upornostjo 300 Ω, tuljave z induktivnostjo 20 mH in kondenzatorja s kapacitivnostjo 0,1 μF, priključimo na sinusno napetost 5 V/5,3 kHz (sl. 3.2.6).

Z merjenjem ugotovimo, da so efektivne napetosti na elementih kroga:

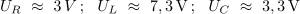
Primerjava aritmetične vsote efektivnih napetosti na elementih z napetostjo izvora pa pove:

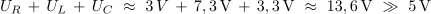
V primeru poskusa 3.2.2 je že sam padec napetosti na tuljavi večji od napetosti izvora, kar daje slutiti še kakšno zanimivost tovrstne vezave.

Kazalčni diagram napetosti in toka

Kazalec skupne količine – toka I – narišemo na pozitivno vodoravno os koordinatnega sistema (sl. 3.2.7). Kazalce napetosti v krogu narišemo na enakih osnovah in na enak način kot v izmeničnem krogu z zaporedno vezavo upora in tuljave s tem, da na podoben način upoštevamo še vpliv kondenzatorja.

V izmeničnem krogu z zaporedno vezavo upora, tuljave in kondenzatorja sta kazalca padcev napetosti na tuljavi in kondenzatorju pravokotna na kazalec napetosti na uporu in nasprotno usmerjena.
Padca napetosti na tuljavi in kondenzatorju sta v protifazi (medsebojni fazni premik med njima je 180 º).
Efektivna napetost izvora je enaka geometrični vsoti efektivnih napetosti na uporu, tuljavi in kondenzatorju.

Geometrično vsoto kazalcev napetosti dobimo najpreprosteje tako, da najprej zaradi nasprotne usmerjenosti aritmetično odštejemo kazalca napetosti U_L in U_C, kazalec razlike U_L – U_C pa geometrično prištejemo kazalcu napetosti U_R.

Razmerje napetosti na induktivni in kapacitivni upornosti je odvisno od razmerja induktivne in kapacitivne upornosti. Možni so trije splošni primeri:

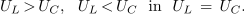
Kazalčne diagrame za navedene tri primere primerjalno prikazuje slika 3.2.8 a), b) in c):

V izmeničnem krogu z zaporedno vezavo upora, tuljave in kondenzatorja tok lahko prehiteva, zaostaja ali pa je v fazi z napetostjo izvora.
Zaporedna vezava upora, tuljave in kondenzatorja ima lahko značaj in lastnosti zaporedne vezave upora in tuljave, upora in kondenzatorja ali samo upora.
Fazni kot izmeničnega kroga z zaporedno vezavo upora, tuljave in kondenzatorja ima lahko poljubno vrednost med - 90 º in + 90 º.

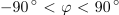
Trikotnik napetosti in upornosti

Iz sl. 3.2.8 so razvidni trije možni splošni primeri značaja izmeničnega kroga z zaporedno vezavo upora, tuljave in kondenzatorja. Iz praktičnih razlogov se za nadaljnjo obravnavo odločimo za vezavo z induktivnim značajem (sl. 3.2.9):

Iz kazalčnega diagrama lahko izrišemo pravokotni trikotnik napetosti s stranicami U, U_R in U_L – U_C (sl. 3.2.9 a). Če stranice napetostnega trikotnika delimo še s skupno količino zaporednega kroga, s tokom I,

dobimo trikotnik upornosti (sl. 3.2.9 b).

Napetosti in upornosti zaporednega kroga z uporom, tuljavo in kondenzatorjem tvorijo pravokotna trikotnika. Seštevamo jih geometrično.

Zaradi enostavnosti bomo pri obravnavi napetostnih trikotnikov sicer operirali z efektivnimi vrednostmi napetosti. Vemo pa, da napetostni trikotnik velja tudi za maksimalne vrednosti sinusne napetosti.

Računanje količin v zaporednem krogu z uporom, tuljavo in kondenzatorjem temelji torej na enakih pravilih kot v zaporednem krogu z upornostjo in tuljavo ali kondenzatorjem. Dodatno dejstvo je v nasprotni kateti trikotnika, ki je v tem primeru razlika dveh jalovih napetosti ali upornosti. Tudi v tem primeru lahko po Pitagorovem izreku zapišemo npr.:

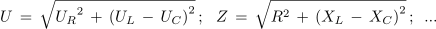
in kotne funkcije, npr.:

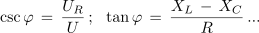
Navedene in druge enačbe reševanja pravokotnega trikotnika omogočajo pri dveh znanih količinah trikotnika računanje tretje količine.

Preskusimo prvo od dobljenih enačb na rezultatih meritev poskusa 3.2.2:

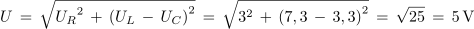
V primeru enakosti induktivne in kapacitivne upornosti ima obravnavani krog poleg lastnosti

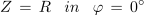
še druge zanimive lastnosti, ki pa jih bomo obravnavali v okviru poglavja o resonančnih^[1] pojavih.

Primera:

Primer:

1. Zaporedna vezava upora z upornostjo 30 Ω, tuljave z induktivnostjo 2 H in kondenzatorja s kapacitivnostjo 6 μF, je priključena na izmenično napetost 230 V/50 Hz. Izračunaj tok in padce napetosti v električnem krogu. Kolikšen bi bil tok, če bi frekvenco spremenili tako, da bi se kapacitivna in induktivna upornost izenačili?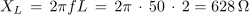

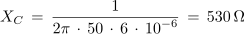
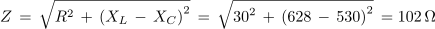
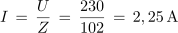
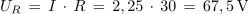
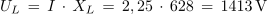
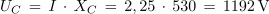
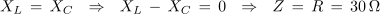
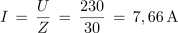
Rešitev

Primer:

2. Kolikšna mora biti kapacitivnost kondenzatorja, ki ga vežemo zaporedno z uporom z upornostjo 82 Ω in tuljavo z induktivnostjo 0,1 H, če želimo, da bo pri krožni frekvenci 10 4 s^-1 vezava elementov povzročala fazni kot 25 º?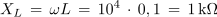

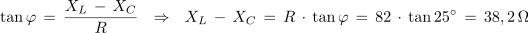
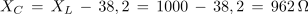
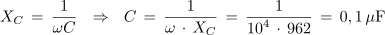
Rešitev

Preskusi svoje znanje

1. Kaj je impedanca in kaj admitanca?

2. Od česa je odvisna in kaj povzroča impedanca?

3. Ali je tudi v zaporednih izmeničnih krogih napetost izvora enaka aritmetični vsoti padcev napetosti na elementih kroga? Pojasni!

4. V zaporednem izmeničnem krogu z uporom in tuljavo povečamo frekvenco napetosti izvora. Ali se bo kaj zgodilo z napetostmi na uporu in tuljavi? Pojasni!

5. V zaporednem izmeničnem krogu z uporom in kondenzatorjem podvojimo frekvenco napetosti izvora in kapacitivnost kondenzatorja. Ali ima to kakšen vpliv na tok in fazni kot v krogu? Pojasni!

6. Katero količino zaporednega izmeničnega kroga (U, I, Z ...) izberemo kot izhodiščno količino pri risanju kazalčnega diagrama kroga? Zakaj?

7. Ali je tudi v zaporednih izmeničnih krogih skupna upornost v krogu (impedanca) enaka aritmetični vsoti upornosti posameznih elementov kroga? Pojasni!

8. Kako dobimo trikotnike napetosti in upornosti poljubnega zaporednega izmeničnega kroga?

9. Katera matematična pravila nam pomagajo pri računanju količin v zaporednih izmeničnih krogih? Pojasni!

10. Zakaj so trikotniki količin zaporednih izmeničnih krogov vedno pravokotni?

11. Kaj je VAr in kaj Q?

12. Od česa je odvisno razmerje med delovno in jalovo energijo v zaporednem izmeničnem krogu?

13. Katere vrednosti lahko ima fazni kot zaporednega izmeničnega kroga?

14. Od česa je odvisen značaj zaporedne vezave elementov v izmeničnem krogu? Pojasni!

15. Kolikšna sta impedanca in fazni kot zaporednega izmeničnega kroga pri pogoju X_L = X_C? Pojasni!

16. Kako določeni induktivnosti in kapacitivnosti dosežemo enakost X_L = X_C?

17. Kako lahko v zaporednem izmeničnem krogu, pri konstantni napetosti izvora ter pogojih R > 0, X_L > 0 in X_C > 0 dosežemo največji tok? Pojasni!

18. Ali so napetosti na ohmskem uporu, tuljavi in kondenzatorju v zaporednem izmeničnem krogu lahko enake ali celo večje od napetosti izvora? Pojasni!

Naloge:

1. Napetost 230 V /50 Hz poganja v zaporednem krogu z uporom in tuljavo tok 2 A. Kolikšna je induktivnost tuljave, če je upornost upora 90 Ω? (L = 228 mH)

2. Kolikšna je impedanca zaporedne vezave upora z upornostjo 400 Ω in tuljave z induktivno upornostjo 600 Ω? Nalogo reši grafično in analitično! (Z = 721 Ω)

3. Impedanca zaporedne vezave upora in tuljave je 100 Ω. Kolikšni sta upornost upora in induktivnost tuljave, če vezava povzroča v izmeničnem krogu fazni kot 60 º? (R = 50 Ω, L = 0.1 mH)

4. Porabnik, ki ima značaj zaporedne vezave upora in tuljave, priključimo na enosmerno napetost 25 V. Tok, ki ga pri tem izmerimo, je 5 A. Porabnik na to priključimo na izmenično napetost 15 V /100 Hz, tok, ki ga pri tem izmerimo, pa je 1 A. Izračunaj delovno upornost, impedanco in induktivnost porabnika! (R = 5 Ω; Z = 15 Ω; L = 22,5 mH)

5. Tok skozi zaporedno vezavo upora z upornostjo 400 Ω in kondenzatorja s kapacitivnostjo 7,5 μF je 100 mA / 50 Hz. Na kolikšno napetost je priključena vezava? (U = 58,3V)

6. Kolikšna mora biti upornost upora, ki ga vežemo zaporedno s kondenzatorjem s kapacitivnostjo 220 μF, če želimo, da bo impedanca vezave 52 Ω? (R = 50 Ω)

7. Izračunaj kapacitivnost kondenzatorja v zaporednem RLC krogu pri L = 0,1 H; R = 82 Ω in ω = 10⁴ s^-1, če je fazni kot, ki ga povzroča vezava, φ = 25 º. (C = 0.1 μF)

8. Kolikšni morata biti induktivnost tuljave in kapacitivnost kondenzatorja zaporedno vezanih z uporom, če želimo, da bosta napetosti na tuljavi in kondenzatorju petkrat večji od napetosti izvora? Upornost upora je 200 Ω, frekvenca napetosti izvora pa 1 kHz. (L = 159 mH; C = 159 nF)