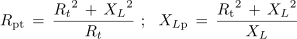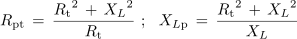7.3.2 Vzporedni električni nihajni krog

Iz e-ELEKTROTEHNIKA plus

Redakcija iz 13:52, 8. maj 2010 od Andrej (Pogovor | prispevki)

(prim) ← Starejša redakcija | poglejte trenutno redakcijo (prim) | Novejša redakcija → (prim)

Vzporedni nihajni krog (slika 7.3.3) je v bistvu izmenični krog z vzporedno vezavo upora, tuljave in kondenzatorja, katerega osnovne lastnosti in zakonitosti že poznamo. Naredimo zato podobno, čeprav nekoliko krajšo pot kot pri zaporednem nihajnem krogu.

Poskus 7.3.4:

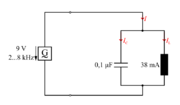
Vzporedno vezavo kondenzatorja s kapacitivnostjo 0.1 μF in tuljave z induktivnostjo 9,5 mH, priključimo na izvor sinusne napetosti 9 V nastavljive frekvence (slika 7.3.11).

Slika 7.3.11

Pri stalni napetosti izvora povečujmo frekvenco napetosti od 2,8 kHz do 8 kHz in pri posamezni frekvenci izmerimo toke kondenzatorja, tuljave in izvora. Dobili bomo vrednosti:

TABELA

Pri določeni frekvenci (5160 Hz) je tok izvora zelo majhen, pri višjih in nižjih frekvencah pa je bistveno večji.
Pri enaki frekvenci (5160 Hz) sta toka kondenzatorja enaka in bistveno večja od toka izvora.

Iz enakosti tokov I_C in I_L lahko glede na znano dejstvo, da sta v proti fazi, sklepamo, da je v našem primeru pri frekvenci 5160 Hz popolna izmenjava energij W_C in W_L med kondenzatorjem in tuljavo. Podobno lahko iz toka izvora sklepamo, da je za vzdrževanje vsiljenega nihanja energije v LC nihajnem krogu pri omenjeni frekvenci potrebno najmanj energije.

Vzporedni LC nihajni krog se na določeno frekvenco vsiljenega nihanja odzove na način, ki je značilen za lastno nihanje.
Frekvenco vsiljenega nihanja, pri kateri je za nihanje energije v vzporednem nihajnem krogu potrebno najmanj energije, imenujemo resonančna frekvenca.
Resonančna frekvenca vzporednega nihajnega kroga je enaka frekvenci lastnega nihanja kroga.

Ker sta pri lastnem nihanju LC nihajnega kroga reaktanci oziroma susceptanci enaki, velja tudi za vsiljeno nihanje vzporednega nihajnega kroga:

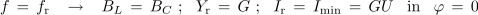
V poskusu 7.3.4 sicer nismo imeli tuljavi in kondenzatorju vzporedno priključenega upora, toda izgubna upornost predvsem tuljave ima podoben učinek. Obstaja enostavna metoda, po kateri zaporedno RL vezavo preračunamo v enakovredno vzporedno RL vezavo^[1]. V našem primeru bi izmerili upornost navitja tuljave ≈ 11 Ω, preračunana enakovredna vzporedna upornost pa bi znašala ≈ 9 kΩ.

Frekvenčna karakteristika toka vzporednega nihajnega kroga

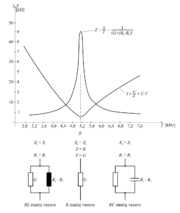
Če rezultate meritev poskusa 7.3.4 prikažemo grafično, dobimo sliko frekvenčne odvisnosti (karakteristiko) toka vzporednega nihajnega kroga (slika 7.3.12).

Vzporedni nihajni krog slabo prepušča tok resonančne frekvence in frekvenc, ki so blizu resonančni frekvenci, tokove višjih in nižjih frekvenc pa bistveno bolje.

Če bi namesto izvora čiste sinusne napetosti na nihajni krog priključili izvor iz množice napetosti različnih frekvenc sestavljene napetosti, bi v nihajnem krogu bili toki višjih in nižjih frekvenc, toki resonančne frekvence in frekvenc, ki so blizu resonančni, pa bi bili močno dušeni.

Slika 7.3.12: Frekvenčna odvisnost toka vzporednega nihajnega kroga

Vzporedni nihajni krog je pasovni, zaporni frekvenčni filter.
Lastnost vzporednega nihajnega kroga, da iz množice možnih tokov različnih frekvenc »izbira« in zaduši le določene tokove, imenujemo selektivnost vzporednega nihajnega kroga.

Filtrske lastnosti vzporednega nihajnega kroga uporabljamo predvsem v radijski in TV tehniki v podobne namene, kot smo jih že omenili pri zaporednem nihajnem krogu.

Resonančno frekvenco vzporednega nihajnega kroga dobimo na podoben način kot za zaporednega, iz pogoja enakosti reaktanc, zato bomo končni izraz kar napisali:

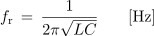
Toda pozor. Če je tuljava slabe kakovosti in bomo njeno nadomestno zaporedno vezavo pretvarjali v vzporedno, bo nekoliko spremenjena tudi induktivna reaktanca. Posledično bo tudi resonančna frekvenca nekoliko drugačna. Navedena enačba pa velja dovolj dobro za kakovosti tuljave večje od 10.

Področje frekvenc, katerih toke vzporedni nihajni krog slabo prevaja, imenujemo zaporni frekvenčni pas nihajnega kroga B (sl. 7.3.13).
Zaporni frekvenčni pas je področje frekvenc, v katerem tok v nihajnem krogu moč P_r ne naraste čez 2P_r oziroma tok ni večji od I_r • √2.
Širina zapornega frekvenčnega pasu B je določena z razliko mejnih frekvenc zapornega področja f_mzg in f_msp.

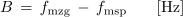
Enačbo za neposredno računanje širine zapornega frekvenčnega pasu B dobimo na podoben način kot pri zaporednem nihajnem krogu.

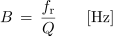
Vidimo, da kljub nasprotnima oblikama frekvenčnih karakteristik toka zaporednega in vzporednega nihajnega kroga obravnavamo njune lastnosti na podoben način.

Kakovost vzporednega nihajnega kroga

Za vzporedni nihajni krog velja enaka definicija kakovosti, le da je v tem primeru skupna količina za računanje moči napetost izvora. Paralelni upor R_p praviloma ni dejanski upor, ampak v paralelno vezavo transformirana izgubna upornost predvsem tuljave^[2].

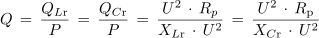
oziroma po ureditvi

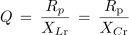
Kakovost vzporednega nihajnega kroga je premo sorazmerna z v paralelno upornost transformirane izgubne upornosti tuljave in obratno sorazmerna z rektancama nihajnega kroga pri resonančni frekvenci.
Vzporedna upornost (prevodnost) zmanjšuje kakovost vzporednega nihajnega kroga in povečuje njegov tok (propustnost) pri resonančni frekvenci.

Tudi navedena enačba je sprejemljiva za kakovosti tuljave večje od 10. Še bolj korektni bi bili, če bi tako pri zaporednem kot pri vzporednem nihajnem krogu pri kakovosti nihajnega kroga upoštevali tudi realnost izvora napetosti.

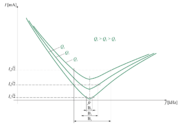
Na osnovi spoznanj pri obravnavi vpliva kakovosti na obliko karakteristike zaporednega nihajnega kroga lahko narišemo frekvenčne karakteristike toka vzporednega nihajnega kroga za različne kakovosti (sl. 7.3.13).

Slika 7.3.13: Vpliv kakovosti na obliko frekvenčne karakteristike toka vzporednega nihajnega kroga

Čim večja je kakovost vzporednega nihajnega kroga, tem manjši je resonančni tok, tem ožji je frekvenčni zaporni pas in tem boljša je selektivnost nihajnega kroga.

Frekvenčna karakteristika admitance vzporednega nihajnega kroga

Frekvenčno karakteristiko admitance Y(f) vzporednega nihajnega kroga lahko dobimo na osnovi izmerjenih tokov pri različnih frekvencah (poskus 7.3.4) in Ohmovega zakona

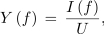
lahko pa tudi z računanjem po izrazu

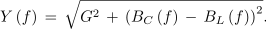
Ob dejstvu, da je U = konst., obliko navedene karakteristike prikazuje slika 7.3.12.

Oblika frekvenčne karakteristike admitance vzporednega nihajnega kroga je podobna obliki frekvenčne karakteristike impedance zaporednega nihajnega kroga.

S sliko frekvenčne karakteristike admitance smo tako le nazorneje prikazali lastnosti vzporedne vezave upora, tuljave in kondenzatorja v izmeničnem krogu.

Tokovna resonanca

V poskusu 7.3.4 smo ugotovili, da sta toka kondenzatorja in tuljave pri resonančni frekvenci vzporednega nihajnega kroga enaka in veliko večja od toka izvora. Kazalčni diagram izmeničnega kroga z vzporedno vezavo upora, tuljave in kondenzatorja potrjuje, da je to mogoče (tokova sta v proti fazi).

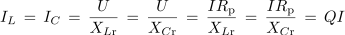
oziroma

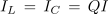
Toka tuljave in kondenzatorja v vzporednem nihajnem krogu sta pri resonančni frekvenci Q - krat večja od toka izvora.
Zaradi »ojačenja« toka imenujemo resonanco vzporednega nihajnega kroga tokovna resonanca.

Tokovno resonanco koristno uporabljamo podobno kot napetostno resonanco na področju elektronike, predvsem radijske, TV in krmilne tehnike. Pri merjenju električnega toka v napravah ali sistemih, katerih frekvenca delovanja je enaka ali blizu resonančni frekvenci, pa moramo biti pozorni na pravilno izbiro merilnega območja A-metra.