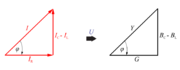Iz e-ELEKTROTEHNIKA plus
Poskus 2.2.4:
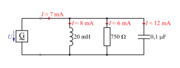
Vzporedno vezavo upora z upornostjo 750 Ω, tuljave z induktivnostjo 20 mH in kondenzatorja s kapacitivnostjo 0,1 µF, priključimo na napetost 4,5 V/4,4 kHz (sl. 3.2.13)
Izmerimo efektivne toke IR, IL, IC in I ter preverimo izmerjeno z zakonom tokovnega vozlišča:
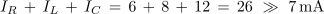
Aritmetična vsota efektivnih tokov je v danem primeru precej večja od efektivnega toka izvora. Nekaj podobnega smo ugotovili tudi pri zaporedni vezavi vseh treh elementov v poskusu 3.2.2, le da smo takrat imeli opravka z napetostmi.
Kazalčni diagram napetosti in tokov
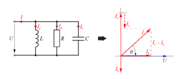
Skupna količina elementom kroga je napetost U, na že znani način pa dobimo kazalčni diagram, ki ga prikazuje sl.3.2.14:
- V vzporednem izmeničnem krogu z uporom, tuljavo in kondenzatorjem sta kazalca tokov tuljave in kondenzatorja nasprotno usmerjena in pravokotna na kazalec toka skozi upor.
- Toka tuljave in kondenzatorja sta v protifazi.
- Efektivni tok izvora je enak geometrični vsoti efektivnih tokov upora, tuljave in kondenzatorja.
Razmerje tokov tuljave in kondenzatorja je odvisno od razmerja induktivne in kapacitivne upornosti. Možni so trije splošni primeri:
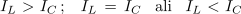
Kazalčne diagrame za navedene tri primere kaže primerjalno slika 3.2.15 a, b in c.
- V izmeničnem krogu z vzporedno vezavo upora, tuljave in kondenzatorja tok lahko prehiteva, zaostaja ali pa je v fazi z napetostjo izvora (podobno kot pri zaporedni vezavi istih elementov).
- Vzporedna vezava upora, tuljave in kondenzatorja ima lahko značaj in lastnosti vzporedne vezave upora in tuljave ali upora in kondenzatorja ali samo upora.
Vzporedna vezava upora, tuljave in kondenzatorja povzroča v izmeničnem krogu fazni kot med - 90 º in + 90 º.
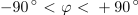
Trikotnik tokov in prevodnosti
Iz kazalčnega diagrama na sl. 3.2.15 izrišemo trikotnik tokov (sl. 3.2.16 a), z deljenjem njegovih stranic s skupno količino elementov U pa dobimo trikotnik prevodnosti vezave (sl. 3.2.16 b).
- Toki in prevodnosti izmeničnega kroga z vzporedno vezavo upora, tuljave in kondenzatorja tvorijo pravokotna trikotnika.
- Toke in prevodnosti vzporedne vezave upora, tuljave in kondenzatorja seštevamo geometrično.
Po pravilih za računanje v pravokotnem trikotniku lahko zapišemo:
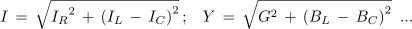
ali tudi

kar pri treh znanih količinah trikotnika omogoča računanje četrte količine.
V medsebojnem odnosu kapacitivne in induktivne prevodnosti in posledično tudi tokov vzporedne vezave elementov (sl. 3.2.15) obstajajo tri možnosti:
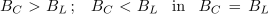
V vseh treh primerih admitanco vezave izračunamo na enak, zgoraj navedeni način. Zanimiv primer nastopi v primeru enakosti

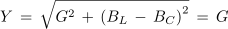
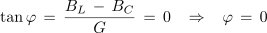
- Admitanca vzporedne vezave upora, tuljave in kondenzatorja je v primeru enakosti njunih jalovih prevodnosti, najmanjša. Enaka je le delovni prevodnosti in ne povzroča faznega premika med napetostjo in tokom izvora.
V primeru enakosti induktivne in kapacitivne prevodnosti ima vzporedni vezava upora, tuljave in kondenzatorja, podobno kot zaporedna vezava, še druge zanimive lastnosti, ki pa jih bomo obravnavali pri resonančnih pojavih.
Primera:
Primer:
1. Vzporedna vezava upora z upornostjo 750 Ω, tuljave z induktivnostjo 20 mH in kondenzatorja s kapacitivnostjo 100 nF je priključena na izvor sinusne napetosti frekvence 5 kHz. Izračunaj admitanco, impedanco ter fazni kot, ki ga vezava povzroča v električnem krogu.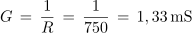
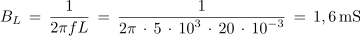
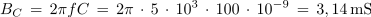
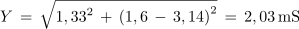
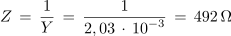
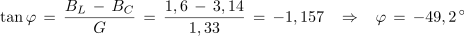
Primer:
2. Izračunaj kapacitivnost kondenzatorja, ki ga moramo vezati vzporedno z vzporedno vezanima uporom z upornostjo 2,7 kΩ in tuljavo z induktivnostjo 200 μH, če želimo, da bo vezava pri krožni frekvenci 2,5 • 106 s-1 povzročala zaostajanje toka za napetostjo za 30 º.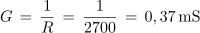
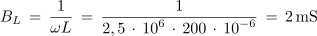
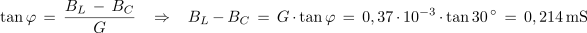
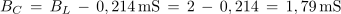
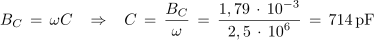
Preizkusi svoje znanje
1. Kako seštevamo toke posameznih elementov v vzporednih izmeničnih krogih? Pojasni.
2. V izmeničnem krogu z vzporedno vezavo upora in kondenzatorja podvojimo frekvenco napetosti izvora, kapacitivnost kondenzatorja pa zmanjšamo na 1/4. Ali ima to kakšen vpliv na tok izvora in fazni kot? Pojasni.
3. Katero količino vzporednega izmeničnega kroga (U, I, Y ...) izberemo kot izhodiščno količino pri risanju kazalčnega diagrama kroga? Zakaj?
4. Kako dobimo trikotnik toka in prevodnosti poljubnega vzporednega izmeničnega kroga?
5. Katera matematična pravila pomagajo pri računanju količin v vzporednih izmeničnih krogih? Pojasni.
6. Katere velikosti ima lahko fazni kot izmeničnega kroga z vzporedno vezavo upora in kondenzatorja?
7. Od česa je odvisen značaj vzporedne vezave upora, tuljave in kondenzatorja? Pojasni.
8. Kolikšna sta admitanca in fazni kot vzporednega izmeničnega kroga pri pogoju BL = BC? Pojasni.
9. Kako lahko dosežemo enakost BL in BC?
10. Ali je kateri od tokov vzporedne vezave upora, tuljave in kondenzatorja lahko večji od toka izvora? Pojasni.
11. Kako lahko pri konstantni napetosti izvora ter konstantni upornosti, induktivnosti in kapacitivnosti vplivamo na velikost toka izvora in dosežemo njegov minimum?
12. Vzporedno vezavo ohmske in induktivne upornosti spremenimo v zaporedno. Kaj se zgodi s faznim kotom?
Naloge:
1. Napetost 5 V / 10 kHz poganja skozi vzporedno vezavo upora in kondenzatorja tok 120 mA. Kolikšna je kapacitivnost kondenzatorja, če je upornost upora 50 Ω? (0,27 μF)
2. Vzporedna vezava upora z upornostjo 15 Ω in tuljave z induktivnostjo 90 mH je priključena na izmenično napetost 100 V /50 Hz. Izračunaj tok izvora in impedanco vezave. (7,5 A; 13,2 Ω)
3. Izračunaj admitanco in fazni kot vzporedne vezave upora z upornostjo 20 k Ω in tuljave z induktivnostjo 200 mH. (50 μS; 89,6 º)
4. Kolikšna mora biti upornost upora v vzporedni vezavi s tuljavo, če naj ta pri induktivnosti tuljave 1 H in frekvenci 1.8 kHz povzroča fazni kot 45 º? (11.3 Ω )
5. Izračunaj admitanco in impedanco ter fazni kot vzporedne vezave upora z upornostjo 40 Ω in kondenzatorja s kapacitivnostjo 2 μF. Frekvenca f je 2 kHz. (35,3 mS; 28,3 Ω; -45 º)
6. Vzporedni vezavi upora z upornostjo R1 = 1 kΩ in tuljave z induktivnostjo L vežemo vzporedno še en upor z upornostjo R2. Kolikšna mora biti upornost R2, če želimo, da bo njena priključitev povzročila zmanjšanje faznega kota 45 º za 10 º? Kolikšen bo fazni kot, če dobljeno upornost R2 vežemo zaporedno z R1? (213 Ω; 50,6 º)
7. Pri kolikšni frekvenci bo vzporedna vezava upora z upornostjo 5,6 kΩ in kondenzatorja s kapacitivnostjo 0,47 μF povzročala fazni kot 45 º? (60,5 Hz)
8. Impedanca vzporedne vezave upora in kondenzatorja je 200 Ω, fazni kot pa -37 º. Izračunaj upornost upora in kapacitivnost kondenzatorja pri krožni frekvenci 3000 s-1. (250 Ω; 1 μF)
9. Vzporedna vezava upora in kondenzatorja s kapacitivnostjo 0,5 μF je priključena na izmenično napetost s krožno frekvenco 4000 s-1. Tok izvora 15 mA, tok kondenzatorja pa 12 mA. Izračunaj upornost in tok upora, napetost izvora ter fazni kot in admitanco vezave. (666 Ω; 9 mA; 6 V; 53,1 º; 2,5 mS)
10. Kolikšno upornost mora imeti upor, ki ga vežemo vzporedno s kondenzatorjem kapacitivnosti 50 nF, če želimo, da bo izmenična napetost 150 V pri krožni frekvenci 5 • 103 s-1 pognala skozi vezavo tok 45 mA? (6 kΩ)
11. V vzporedni vezavi upora, tuljave in kondenzatorja je tok upora 5,5 A / 50 Hz, tok izvora pa zaostaja za napetostjo izvora za fazni kot 45 º. Izračunaj induktivnost tuljave in kapacitivnost kondenzatorja, če je upornost upora 20 Ω, razmerje tokov IC : IL pa 2 : 3. (318 μF; 21,2 mH)
12. Vzporedno vezavo sestavljajo pri krožni frekvenci 1000 s-1 prevodnosti G, BL = 8 mS in BC = 5 mS. Kolikšna je upornost upora, induktivnost tuljave, kapacitivnost kondenzatorja in impedanca, če je fazni kot vezave 45 º?
Podpoglavja:
- 3.2.4.1 Kazalčni diagram napetosti in tokov
- 3.2.4.2 Trikotnik tokov in prevodnosti.
- 3.2.4.3 Vzporedna RLC vezava (interaktivna simulacija)
| | 3.2.4.1 Kazalčni diagram napetosti in tokov |