Iz e-ELEKTROTEHNIKA plus
Slika:OET2 a poglavje 03 slika 03.svg
Amplituda napetosti je približno 325 V, začetni kot okoli -45 °, perioda okoli 20 ms in frekvenca okoli 50 Hz. Po podatkih sodeč pripada časovni diagram harmonični omrežni napetosti.
Slika:OET2 a poglavje 03 slika 04.svg
Vlak ponavljajočih tokovnih impulzov.
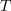

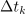
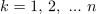
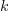
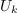
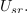

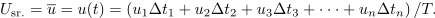
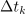
Zgled 2
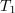

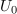
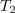
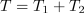
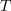
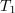
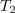
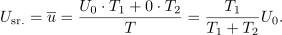
Primer: V času impulza (trajanja 1 ms) naj ima napetost vrednost 10 V; čas pavze naj bo 3 ms. Iz formule sledi srednja vrednost 2,5 V.[3] Srednjo vrednost periodične funkcije geometrijsko interpretira oddaljenost črte od abscise, ki z obeh strani črte izenačuje površine likov med funkcijo in črto.
Srednja vrednost harmonične funkcije
Tokrat imejmo harmonični tok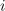
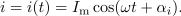
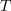
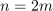
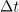
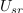
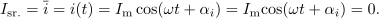
Opombe
- ↑ O vsoti sumandov, ki jih je veliko in imajo neznatne vrednosti, bomo govorili v zadnjem poglavju, v okviru določenega integrala.
- ↑ Multivibrator je posebno elektronsko vezje, ki generira pulzirajočo napetost.
- ↑ In kako bi komentirali ; impulznega toka
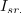 v primeru instrumenta z vrtljivo tuljavico? Ker okorna tuljavica ne more slediti pogostim impulzom toka, se ustali v legi, ki je sorazmerna
v primeru instrumenta z vrtljivo tuljavico? Ker okorna tuljavica ne more slediti pogostim impulzom toka, se ustali v legi, ki je sorazmerna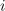
Podpoglavja:
| | 1.1.1.1 Srednja vrednost harmonične funkcije |
