|
|
| (7 intermediate revisions not shown) |
| Vrstica 1: |
Vrstica 1: |
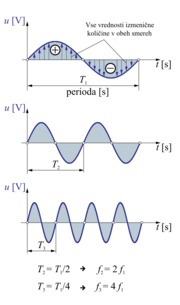
| | + | [[Image:eele_slika_1_8.svg|thumb|right|Slika 1.8: Perioda in frekvenca]] |
| | + | |
| | <poskus> | | <poskus> |
| | '''Poskus 1.2:''' | | '''Poskus 1.2:''' |
| Vrstica 7: |
Vrstica 9: |
| | </poskus> | | </poskus> |
| | | | |
| - |
| |
| - |
| |
| - | == Perioda (''T'') in frekvenca (''f'') ==
| |
| - |
| |
| - | <pomembno>
| |
| - | *Čas, v katerem se zvrstijo vse vrednosti izmenične količine v obeh smereh (slika 1.8), imenujemo perioda<ref>gr. periodos = obhod</ref> (''T'').
| |
| - | *Osnovna enota za merjenje periode je sekunda.
| |
| - | </pomembno>
| |
| - |
| |
| - | Periode izmeničnih količin so lahko različne. To pomeni, da se v enakem času lahko zvrsti različno število period (slika 1.9 b in c).
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Število period v časovni enoti imenujemo frekvenca<ref>lat. frequentia = ponavljanje, pogostost</ref> (''f'').
| |
| - | *Frekvenca je obratno sorazmerna s periodo.
| |
| - | </pomembno>
| |
| - |
| |
| - |
| |
| - | <latex>f = \frac{1}{T} |||(Hz) (1/s = s<sup>-1</sup> = '''hertz''' = '''Hz''') ''T''(s)|||'''Enačba 1.1'''</latex>
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Osnovna enota za merjenje frekvence je s<sup>-1</sup>. Imenujemo jo hertz<ref>Heinrich '''Hertz''', nemški fizik</ref>(Hz).</pomembno>
| |
| - |
| |
| - | Frekvence izmeničnih električnih količin so najpogosteje med nekaj desetink Hz in več sto GHz. Frekvenčno področje možnega sinusnega nihanja energije in njenega širjenja v prostor v obliki elektromagnetnih valov pa je še veliko širše. Skupaj s področji uporabe je prikazano v preglednici 1.1. Podrobneje obravnava valovanje fizika.
| |
| - |
| |
| - | '''Primera:''' <primer>
| |
| - | 1. Kolikšna je perioda sinusne napetosti pri frekvenci 50 Hz?|||
| |
| - | <latex>f = \frac{1}{T}\,\,\,\,\, \Rightarrow \,\,\,\,\,T = \frac{1}{f} = \frac{1}{ {50{\mathrm{\, s} }^{ {\mathrm{-1} } } } } = {\mathrm{0,02\, s} } = {\mathrm{20\, ms} }</latex>
| |
| - | </primer>
| |
| - | <primer>
| |
| - | 2. Kolikšne so periode izmeničnih količin na območju ultravisokih (UHF) frekvenc? Območje UHF je med 300 MHz in 3 GHz (pregl. 1.1).|||
| |
| - | <latex>T_{{\mathrm{max} } } = \frac{1}{ {f_{ {\mathrm{min} } } } } = \frac{1}{ {300 \cdot 10^6 {\mathrm{\, s} }^{ {\mathrm{-1} } } } } = {\mathrm{3,33} } \cdot 10^{-9} {\mathrm{\, s} } = {\mathrm{3,33\,ns} }</latex>
| |
| - | <latex>T_{{\mathrm{min}}} = \frac{1}{{f_{{\mathrm{max}}} }} = \frac{1}{{3 \cdot 10^9 {\mathrm{\, s}}^{{\mathrm{-1}}} }} = {\mathrm{0,333} } \cdot 10^{ - 9} {\mathrm{\, s}} = {\mathrm{0,333\, ns} }</latex>
| |
| - |
| |
| - | </primer>
| |
| - |
| |
| - |
| |
| - |
| |
| - |
| |
| - | == Trenutna vrednost sinusne količine (''u'', ''i'' ...) ==
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Vrednost izmenične količine v določenih trenutkih (''t''<sub>1</sub>, ''t''<sub>2</sub> ... sl. 1.9) imenujemo trenutna vrednost. Označujemo jo z malimi poševno pisanimi črkami ('''''u''''', '''''i''''' ... ).</pomembno>
| |
| - |
| |
| - | V trenutkih ''t''<sub>2</sub> in ''t''<sub>4</sub> – sl. 1.9, je trenutna vrednost izmenične količine '''največja'''. Ta vrednost je merodajna za največje trenutne vrednosti npr. '''električne poljske jakosti '''in dimenzioniranje električne izolacije vodnikov, '''gostote magnetnega pretoka''' in magnetnih sil ...
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Največji trenutni vrednosti izmenične količine pravimo maksimalna vrednost. Označujemo jo z veliko poševno črko in indeksom »m« (''U''<sub>m</sub>, ''l''<sub>m</sub>, ''P''<sub>m</sub> ...).</pomembno>
| |
| - |
| |
| - |
| |
| - |
| |
| - |
| |
| - | == Zapis trenutne vrednosti sinusne količine ==
| |
| - |
| |
| - | Fizikalne količine so znanstveniki opredelili tako, da jih lahko '''merimo''' in '''računamo'''. Čeprav je sinusna oblika izmeničnih količin tista, s katero to naredimo najenostavneje, pa sl. 1.9 pove, da tako enostavno, kot z enosmernimi količinami, gotovo ne gre. Za računanje s sinusno količino pa najprej potrebujemo njen '''matematični zapis'''. Po podobi kroga enote (sl. 1.10) je na sl. 1.11 narisan krog, katerega polmer je določen s '''kazalcem''' »dolžine<ref>v merilu, npr. 100 V ≡ 1 cm oziroma 100 V/cm</ref>« '''''U'''''<sub>max</sub>. Če kazalec '''''U'''''<sub>max</sub> zavrtimo iz položaja po sl. 1.11 v nasprotni smeri urinega kazalca, bosta kot in kotu pripadajoča nasprotna kateta pravokotnega trikotnika naraščala. Pri kotu ''α'' = 90 ° doseže kateta »dolžino« '''''U'''''<sub>max</sub>, z nadaljnjim naraščanjem kota se začne njena dolžina zmanjševati … Grafični potek take odvisnosti katete od kota (sl. 1.12 b) ima sinusno obliko. Trenutno vrednost sinusne količine lahko torej zapišemo in računamo z enačbami, kot sta en. 1.2 in 1.3:
| |
| - |
| |
| - |
| |
| - | <latex> u = U_{\mathrm{max}} \cdot {\mathrm{sin}} \,\alpha |||(V) ali tudi|||'''Enačba 1.2''' </latex>
| |
| - | <latex> i = I_{\mathrm{max}} \cdot {\mathrm{sin}} \,\alpha |||(A) |||'''Enačba 1.3''' </latex>
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Trenutna vrednost sinusne količine ''u'', ''i'', ... je določena s produktom maksimalne vrednosti sinusne količine ''U''<sub>m</sub>, ''I''<sub>m</sub> ... in '''sinusa''' trenutnega kota '''''α'''''.</pomembno>
| |
| - |
| |
| - | '''Primer:'''
| |
| - | <primer>Izračunaj trenutne vrednosti sinusne napetosti katere maksimalna vrednost ja 100 V, pri kotih 0 °, 30 °, 60 ° in 90 °.|||
| |
| - | <latex>u_{\,}\,=\,U_{\mathrm{max}}\,\cdot\,{\mathrm{sin}}\,\,\alpha</latex>
| |
| - | <latex>u_{0}\,=\,100\,\cdot\,{\mathrm{sin\,0}}^{\,\mathrm{o}}\,=\,100\,\cdot\,0\,=\,\mathrm{0\,V}</latex>
| |
| - | <latex>u_{30}\,=\,100\,\cdot\,{\mathrm{sin\,30}}^{\,\mathrm{o}}\,=\,100\,\cdot\,0,5\,=\,\mathrm{50\,V}</latex>
| |
| - | <latex>u_{60}\,=\,100\,\cdot\,{\mathrm{sin\,60}}^{\,\mathrm{o}}\,=\,100\,\cdot\,0,866\,=\,\mathrm{86,6\,V}\,=\,\mathrm{\,}u_{120}</latex>
| |
| - | <latex>u_{90}\,=\,100\,\cdot\,{\mathrm{sin\,90}}^{\,\mathrm{o}}\,=\,100\,\cdot\,1\,=\,\mathrm{100\,V}\,=\,u_{270}</latex>
| |
| - |
| |
| - | Kot '''''α'''''(°) ni enostavno merljiv ali kako drugače določljiv. Zato bomo v nadaljevanju enačbi 1.2 in 1.3 preuredili v obliko, ki kot α izraža z '''merljivima''' količinama – '''frekvenco''' sinusne količine in '''časom'''.</primer>
| |
| - |
| |
| - |
| |
| - |
| |
| - |
| |
| - | == Kako dobimo sinusno električno napetost? ==
| |
| - |
| |
| - |
| |
| - | Najpogostejši načini pridobivanja sinusne napetosti so predvsem:
| |
| - | <pomembno>
| |
| - | *z elektromagnetno indukcijo v navitjih '''rotacijskih generatorjev''' (elektroenergetika), <informacije>, sl. 1.12.
| |
| - | *s pretakanjem in pretvarjanjem magnetne energije v električno in obratno<ref>naraven način nastajanja sinusne napetosti</ref> v '''električnih oscilatorjih''' (elektronika),
| |
| - | *s '''pretvorniki''' enosmerne napetosti npr. fotonapetostnih generatorjev (omrežne sončne elektrarne) in s '''funkcijskimi generatorji''' (elektronika).</pomembno>
| |
| - |
| |
| - | Pri obravnavi izmeničnih električnih količin se bomo najpogosteje srečavali s '''sinusno''' obliko. Zato se dogovorimo, da bomo z izrazom »'''izmenične'''« imeli v mislih '''sinusne''' količine. Pri vsaki drugačni obliki pa bomo to posebej poudarili.
| |
| - |
| |
| - |
| |
| | | | |
| - | <references />
| |
| | {{Hierarchy footer}} | | {{Hierarchy footer}} |