Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
| (4 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
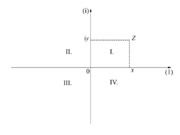
| - | [[Slika: | + | [[Slika:eele_slika_visji_009.svg|thumb|Slika 9: Kompleksno število <latex>z</latex> je točka v kompleksni oziroma Gaussovi ravnini štirih kvadrantov.]] |
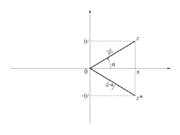
| - | [[Slika: | + | [[Slika:eele_slika_visji_010.svg|thumb|Slika 10: Kompleksno število <latex>z</latex> , njemu konjugirano število <latex>z*</latex>, absolutna vrednost <latex>{\mathrm{abs}(z)}</latex> in argument <latex>{\mathrm{arg}(z)}</latex> kompleksnega števila.]] |
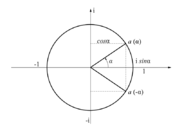
| + | [[Image:eele_slika_visji_011.svg|thumb|Slika 11: Konjugirani števili <latex>a(\alpha)</latex> in <latex>a(-\alpha)</latex> ležita na enotini krožnici polmera 1.]] | ||
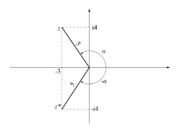
| + | [[Image:eele_slika_visji_012.svg|thumb|Slika 12: Konjugirani števili ležita v II. in III. kvadrantu; razlikujeta se le v imaginarnem delu, imata pa enaki absolutni vrednosti.]] | ||
Vpeljavo števil terjajo računske operacije. Brez celih števil »ni odštevanja« in brez ulomljenih ali racionalnih »ni deljenja«. Po novi razširitvi kliče korenjenje: kvadratni koren pozitivnega števila ni več nujno racionalno, ampak more biti celo iracionalno; racionalna in iracionalna tvorijo realna števila. Za nov »zaplet« poskrbi kvadratni koren (negativnega) števila <latex>-k, k>0</latex>; ni moč najti realnega števila, katerega kvadrat bi bil enak <latex>-k</latex>. Z vpeljavo imaginarne enote <latex>\mathrm{i}</latex> na način, da velja zanjo enačba | Vpeljavo števil terjajo računske operacije. Brez celih števil »ni odštevanja« in brez ulomljenih ali racionalnih »ni deljenja«. Po novi razširitvi kliče korenjenje: kvadratni koren pozitivnega števila ni več nujno racionalno, ampak more biti celo iracionalno; racionalna in iracionalna tvorijo realna števila. Za nov »zaplet« poskrbi kvadratni koren (negativnega) števila <latex>-k, k>0</latex>; ni moč najti realnega števila, katerega kvadrat bi bil enak <latex>-k</latex>. Z vpeljavo imaginarne enote <latex>\mathrm{i}</latex> na način, da velja zanjo enačba | ||
| Vrstica 25: | Vrstica 27: | ||
| - | Slavni nemški matematik Johann Carl Friedrich Gauss je vpeljal ''kompleksno'', po njem imenovano ''Gaussovo ravnino''; opredeljujeta jo ''realna'' in ''imaginarna'' os. Ravnina omogoča predstavitev kompleksnega števila <latex>z=x+{\rm{i}}y</latex> s »točko«; koordinati te točke sta <latex>x</latex> in <latex>{\rm{i}}y</latex> (slika | + | Slavni nemški matematik Johann Carl Friedrich Gauss je vpeljal ''kompleksno'', po njem imenovano ''Gaussovo ravnino''; opredeljujeta jo ''realna'' in ''imaginarna'' os. Ravnina omogoča predstavitev kompleksnega števila <latex>z=x+{\rm{i}}y</latex> s »točko«; koordinati te točke sta <latex>x</latex> in <latex>{\rm{i}}y</latex> (slika 9). Presečišče osi upodablja število ''nič'' (<latex>0 + {\rm{i}}0 = 0</latex>). Osi razdelita ravnino na I., II., III. in IV. ''kvadrant''; te štejemo od desnega zgornjega v levo okoli točke nič (v ''pozitivni matematični smeri''). |
| Vrstica 55: | Vrstica 57: | ||
| - | Upodablja jo daljica med izhodiščem in točko <latex>z</latex>, ki s pozitivnim delom realne osi oklepa kot <latex>\alpha</latex>, z daljicama dolžine <latex>|x|</latex> in <latex>|y|</latex> pa oblikuje pravokoten trikotnik (slika | + | Upodablja jo daljica med izhodiščem in točko <latex>z</latex>, ki s pozitivnim delom realne osi oklepa kot <latex>\alpha</latex>, z daljicama dolžine <latex>|x|</latex> in <latex>|y|</latex> pa oblikuje pravokoten trikotnik (slika 10). Iz trigonometričnih relacij, ki veljajo v pravokotnem trikotniku, dobimo realni in imaginarni del števila <latex>z</latex>: |
| - | <latex>{x = {\mathrm {Re} } (z) = \left| z \right|{\mathrm{cos} }\alpha}</latex> in <latex>{y = {\mathrm {Im} } (z) = \left| z \right|\sin \alpha | + | <latex>{x = {\mathrm {Re} } (z) = \left| z \right|{\mathrm{cos} }\alpha}</latex> in <latex>{y = {\mathrm {Im} } (z) = \left| z \right|\sin \alpha .}</latex> |
| Vrstica 76: | Vrstica 78: | ||
| - | + | Ponuja pa se tudi priložnost, da zapišemo število <latex>z</latex> še v ''trigonometrični'' obliki: | |
| Vrstica 88: | Vrstica 90: | ||
| - | Predstavljata konjugirani števili, <latex>a(\alpha)</latex> in <latex>a(-\alpha)</latex>, ki ležita na enotini krožnici polmera 1 (slika | + | Predstavljata konjugirani števili, <latex>a(\alpha)</latex> in <latex>a(-\alpha)</latex>, ki ležita na enotini krožnici polmera 1 (slika 11). |
| - | '''Zgled 1 | + | '''Zgled 1 ''' |
| - | Dano je kompleksno število: <latex>z = 3 - {\rm{i}}4</latex> (slika | + | Dano je kompleksno število: <latex>z = 3 - {\rm{i}}4</latex> (slika 12). Določimo število <latex>z*</latex>, absolutno vrednost in argument. ⇒ V smislu opredelitev sledijo odgovori: |
Trenutna redakcija s časom 16:37, 12. julij 2010
Vpeljavo števil terjajo računske operacije. Brez celih števil »ni odštevanja« in brez ulomljenih ali racionalnih »ni deljenja«. Po novi razširitvi kliče korenjenje: kvadratni koren pozitivnega števila ni več nujno racionalno, ampak more biti celo iracionalno; racionalna in iracionalna tvorijo realna števila. Za nov »zaplet« poskrbi kvadratni koren (negativnega) števila
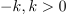
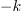
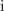
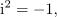
se ponuja nadaljevanje:
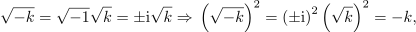
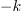
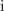
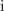

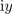
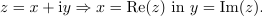

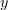


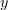

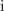
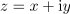

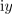

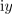
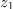
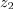
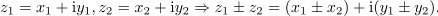
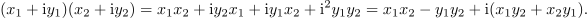

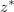

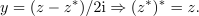

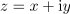
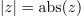
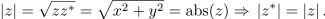

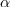
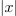
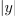

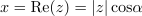
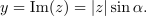
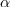
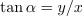


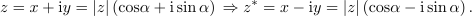
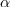
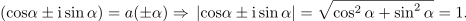
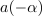
Zgled 1
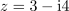
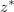
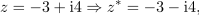
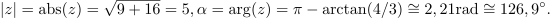
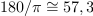
Podpoglavja:
- 1.3.1 Kompleksna količina in kazalec
- 1.3.2 Kazalec harmonične količine
- 1.3.3 Grafično seštevanje (odštevanje) kazalcev
- 1.3.4 »Prehitevanje in zaostajanje kazalcev«
- 1.3.5 Grafično množenje (deljenje) kazalcev
- 1.3.6 Množenje in deljenje z »j«
- 1.3.7 Eulerjeva formula
| | 1.3.1 Kompleksna količina in kazalec |