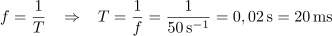e
ELEKTROTEHNIKA
plus
Glavna stran
Kazalo (osnovni nivo)
Kazalo (višji nivo)
Predstavitev projekta
Minimalne zahteve

1.1.3 Osnovne značilnosti izmeničnih količin

1 Osnovni pojmi izmeničnih električnih količin
 >> 
1.1 Izmenične in sestavljene električne količine
 >> 

Iz e-ELEKTROTEHNIKA plus

(Primerjava redakcij)
Skoči na: navigacija, iskanje
Vrstica 14: Vrstica 14:
<pomembno>
<pomembno>
-
*Čas, v katerem se zvrstijo vse vrednosti izmenične količine v obeh smereh (slika 1.8), imenujemo perioda<ref>gr. periodos = obhod</ref> (''T'').
+
*Čas, v katerem se zvrstijo vse vrednosti izmenične količine v obeh smereh (slika 1.8), imenujemo perioda<ref>periodos, gr. = obhod</ref> (''T'').
*Osnovna enota za merjenje periode je sekunda.  
*Osnovna enota za merjenje periode je sekunda.  
</pomembno>  
</pomembno>  
Vrstica 22: Vrstica 22:
   
   
<pomembno>
<pomembno>
-
*Število period v časovni enoti imenujemo frekvenca<ref>lat. frequentia = ponavljanje, pogostost</ref> (''f'').
+
*Število period v časovni enoti imenujemo frekvenca<ref>frequentia, lat. = ponavljanje, pogostost</ref> (''f'').
*Frekvenca je obratno sorazmerna s periodo.  
*Frekvenca je obratno sorazmerna s periodo.  
</pomembno>  
</pomembno>  
Vrstica 35: Vrstica 35:
Frekvence izmeničnih električnih količin so najpogosteje med nekaj desetink Hz in več sto GHz. Frekvenčno področje možnega sinusnega nihanja energije in njenega širjenja v prostor v obliki elektromagnetnih valov pa je še veliko širše. Skupaj s področji uporabe je prikazano v preglednici 1.1. Podrobneje obravnava valovanje fizika.  
Frekvence izmeničnih električnih količin so najpogosteje med nekaj desetink Hz in več sto GHz. Frekvenčno področje možnega sinusnega nihanja energije in njenega širjenja v prostor v obliki elektromagnetnih valov pa je še veliko širše. Skupaj s področji uporabe je prikazano v preglednici 1.1. Podrobneje obravnava valovanje fizika.  
-
'''Primera:''' <primer>
+
'''Primera:'''  
 +
<primer>
1. Kolikšna je perioda sinusne napetosti pri frekvenci 50 Hz?|||
1. Kolikšna je perioda sinusne napetosti pri frekvenci 50 Hz?|||
<latex>f = \frac{1}{T}\,\,\,\,\, \Rightarrow \,\,\,\,\,T = \frac{1}{f} = \frac{1}{ {50{\mathrm{\, s} }^{ {\mathrm{-1} } } } } = {\mathrm{0,02\, s} } = {\mathrm{20\, ms} }</latex>
<latex>f = \frac{1}{T}\,\,\,\,\, \Rightarrow \,\,\,\,\,T = \frac{1}{f} = \frac{1}{ {50{\mathrm{\, s} }^{ {\mathrm{-1} } } } } = {\mathrm{0,02\, s} } = {\mathrm{20\, ms} }</latex>
Vrstica 77: Vrstica 78:
'''Primer:'''  
'''Primer:'''  
-
<primer>Izračunaj trenutne vrednosti sinusne napetosti katere maksimalna vrednost ja 100 V, pri kotih 0 °, 30 °, 60 ° in 90 °.|||
+
<primer>Izračunaj trenutne vrednosti sinusne napetosti, katere maksimalna vrednost ja 100 V, pri kotih 0 °, 30 °, 60 ° in 90 °.|||
<latex>u_{\,}\,=\,U_{\mathrm{max}}\,\cdot\,{\mathrm{sin}}\,\,\alpha</latex>
<latex>u_{\,}\,=\,U_{\mathrm{max}}\,\cdot\,{\mathrm{sin}}\,\,\alpha</latex>
<latex>u_{0}\,=\,100\,\cdot\,{\mathrm{sin\,0}}^{\,\mathrm{o}}\,=\,100\,\cdot\,0\,=\,\mathrm{0\,V}</latex>
<latex>u_{0}\,=\,100\,\cdot\,{\mathrm{sin\,0}}^{\,\mathrm{o}}\,=\,100\,\cdot\,0\,=\,\mathrm{0\,V}</latex>
Vrstica 84: Vrstica 85:
<latex>u_{90}\,=\,100\,\cdot\,{\mathrm{sin\,90}}^{\,\mathrm{o}}\,=\,100\,\cdot\,1\,=\,\mathrm{100\,V}\,=\,u_{270}</latex>
<latex>u_{90}\,=\,100\,\cdot\,{\mathrm{sin\,90}}^{\,\mathrm{o}}\,=\,100\,\cdot\,1\,=\,\mathrm{100\,V}\,=\,u_{270}</latex>
-
Kot '''''α'''''(°) ni enostavno merljiv ali kako drugače določljiv. Zato bomo v nadaljevanju enačbi 1.2 in 1.3 preuredili v obliko, ki kot α izraža z '''merljivima''' količinama – '''frekvenco''' sinusne količine in '''časom'''.</primer>  
+
Kot '''''α''''' (°) ni enostavno merljiv ali kako drugače določljiv. Zato bomo v nadaljevanju enačbi 1.2 in 1.3 preuredili v obliko, ki kot α izraža z '''merljivima''' količinama – s '''frekvenco''' sinusne količine in '''časom'''.</primer>  
   
   

Redakcija: 09:20, 7. maj 2010

Slika 1.8: Perioda in frekvenca

Poskus 1.2:

Poskus 1.1 ponovimo pri frekvencah 0,4 in 4 Hz, po tem pa še pri 50, 100 in 200 Hz.

  • Kazalec analognega merilnika že pri frekvencah nekaj Hz ne more več slediti izmenični količini.
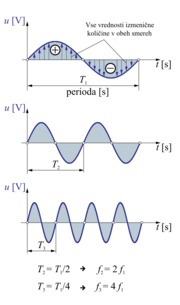
  • Oscilogram izmenične količine postane pri frekvencah, višjih od nekaj deset Hz (sl. 1.8 a, b, c), za oko zvezni potek.


Perioda (T) in frekvenca (f)

  • Čas, v katerem se zvrstijo vse vrednosti izmenične količine v obeh smereh (slika 1.8), imenujemo perioda[1] (T).
  • Osnovna enota za merjenje periode je sekunda.

Periode izmeničnih količin so lahko različne. To pomeni, da se v enakem času lahko zvrsti različno število period (slika 1.9 b in c).


  • Število period v časovni enoti imenujemo frekvenca[2] (f).
  • Frekvenca je obratno sorazmerna s periodo.



  • Osnovna enota za merjenje frekvence je s-1. Imenujemo jo hertz[3](Hz).

Frekvence izmeničnih električnih količin so najpogosteje med nekaj desetink Hz in več sto GHz. Frekvenčno področje možnega sinusnega nihanja energije in njenega širjenja v prostor v obliki elektromagnetnih valov pa je še veliko širše. Skupaj s področji uporabe je prikazano v preglednici 1.1. Podrobneje obravnava valovanje fizika.

Primera:

Primer:

1. Kolikšna je perioda sinusne napetosti pri frekvenci 50 Hz?
Rešitev

Primer:

2. Kolikšne so periode izmeničnih količin na območju ultravisokih (UHF) frekvenc? Območje UHF je med 300 MHz in 3 GHz (pregl. 1.1).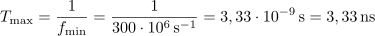
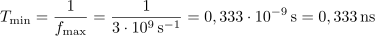
Rešitev





Trenutna vrednost sinusne količine (u, i ...)

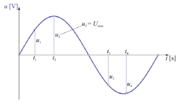
Slika 1.9: Trenutna in maksimalna vrednost
  • Vrednost izmenične količine v določenih trenutkih (t1, t2 ... sl. 1.9) imenujemo trenutna vrednost. Označujemo jo z malimi poševno pisanimi črkami (u, i ... ).

V trenutkih t2 in t4 – sl. 1.9, je trenutna vrednost izmenične količine največja. Ta vrednost je merodajna za največje trenutne vrednosti npr. električne poljske jakosti in dimenzioniranje električne izolacije vodnikov, gostote magnetnega pretoka in magnetnih sil ...


  • Največji trenutni vrednosti izmenične količine pravimo maksimalna vrednost. Označujemo jo z veliko poševno črko in indeksom »m« (Um, lm, Pm ...).



Zapis trenutne vrednosti sinusne količine

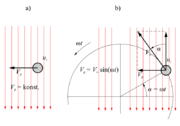
Fizikalne količine so znanstveniki opredelili tako, da jih lahko merimo in računamo. Čeprav je sinusna oblika izmeničnih količin tista, s katero to naredimo najenostavneje, pa sl. 1.9 pove, da tako enostavno, kot z enosmernimi količinami, gotovo ne gre. Za računanje s sinusno količino pa najprej potrebujemo njen matematični zapis. Po podobi kroga enote (sl. 1.10) je na sl. 1.11 narisan krog, katerega polmer je določen s kazalcem »dolžine[4]« Umax. Če kazalec Umax zavrtimo iz položaja po sl. 1.11 v nasprotni smeri urinega kazalca, bosta kot in kotu pripadajoča nasprotna kateta pravokotnega trikotnika naraščala. Pri kotu α = 90 ° doseže kateta »dolžino« Umax, z nadaljnjim naraščanjem kota se začne njena dolžina zmanjševati … Grafični potek take odvisnosti katete od kota (sl. 1.12 b) ima sinusno obliko. Trenutno vrednost sinusne količine lahko torej zapišemo in računamo z enačbami, kot sta en. 1.2 in 1.3:



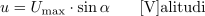
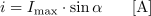
  • Trenutna vrednost sinusne količine u, i, ... je določena s produktom maksimalne vrednosti sinusne količine Um, Im ... in sinusa trenutnega kota α.

Primer:

Primer:

Izračunaj trenutne vrednosti sinusne napetosti, katere maksimalna vrednost ja 100 V, pri kotih 0 °, 30 °, 60 ° in 90 °.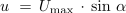
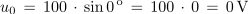
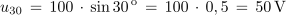
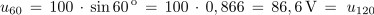
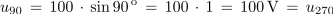
Rešitev









Kot α (°) ni enostavno merljiv ali kako drugače določljiv. Zato bomo v nadaljevanju enačbi 1.2 in 1.3 preuredili v obliko, ki kot α izraža z merljivima količinama – s frekvenco sinusne količine in časom.



Kako dobimo sinusno električno napetost?

Slika 1.12: Elektromagnetna indukcija napetosti

Najpogostejši načini pridobivanja sinusne napetosti so predvsem:

  • z elektromagnetno indukcijo v navitjih rotacijskih generatorjev (elektroenergetika), <informacije>, sl. 1.12.
  • s pretakanjem in pretvarjanjem magnetne energije v električno in obratno[5] v električnih oscilatorjih (elektronika),
  • s pretvorniki enosmerne napetosti npr. fotonapetostnih generatorjev (omrežne sončne elektrarne) in s funkcijskimi generatorji (elektronika).

Pri obravnavi izmeničnih električnih količin se bomo najpogosteje srečavali s sinusno obliko. Zato se dogovorimo, da bomo z izrazom »izmenične« imeli v mislih sinusne količine. Pri vsaki drugačni obliki pa bomo to posebej poudarili.


Opombe

  1. ↑ periodos, gr. = obhod
  2. ↑ frequentia, lat. = ponavljanje, pogostost
  3. ↑ Heinrich Hertz, nemški fizik
  4. ↑ v merilu, npr. 100 V ≡ 1 cm oziroma 100 V/cm
  5. ↑ naraven način nastajanja sinusne napetosti

Podpoglavja:


1.1.2 Sinusna oblika časovnih potekov 1.1.3.1 Perioda in frekvenca
Vzpostavljeno iz »http://eele.tsckr.si/wiki/index.php/Osnovne_zna%C4%8Dilnosti_izmeni%C4%8Dnih_koli%C4%8Din«

Osebna orodja