Iz e-ELEKTROTEHNIKA plus
| Vrstica 46: | Vrstica 46: | ||
| - | delovno kot aritmetično vsoto delovnih faznih moči | + | delovno kot aritmetično vsoto delovnih faznih moči |
| - | <latex>P\, = \,{P_1}\, + \,{P_2} \,+\, {P_3}\, = \,{U_{1{\rm{N}}}}{I_1}\,\cos {\varphi _1}\, +\, {U_{2{\rm{N}}}}{I_2}\,\cos {\varphi _2} \,+ {U_{3{\rm{N}}}}{I_3}\,\cos {\varphi _3}</latex> | + | <latex>P\, = \,{P_1}\, + \,{P_2} \,+\, {P_3}\, = \,{U_{1{\rm{N}}}}{I_1}\,\cos {\varphi _1}\, +\, {U_{2{\rm{N}}}}{I_2}\,\cos {\varphi _2} \,+ {U_{3{\rm{N}}}}{I_3}\,\cos {\varphi _3},</latex> |
| Vrstica 55: | Vrstica 55: | ||
| - | <latex>P \,= \,{Q_1}\, + \,{Q_2}\, + \,{Q_3}\, = \,{U_{1{\rm{N}}}}{I_1}\,\sin {\varphi _1} \,+\, {U_{2{\rm{N}}}}{I_2}\,\sin {\varphi _2}\, + \,{U_{3{\rm{N}}}}{I_3}\,\sin {\varphi _3}</latex> | + | <latex>P \,= \,{Q_1}\, + \,{Q_2}\, + \,{Q_3}\, = \,{U_{1{\rm{N}}}}{I_1}\,\sin {\varphi _1} \,+\, {U_{2{\rm{N}}}}{I_2}\,\sin {\varphi _2}\, + \,{U_{3{\rm{N}}}}{I_3}\,\sin {\varphi _3}.</latex> |
| Vrstica 61: | Vrstica 61: | ||
| - | <latex>\underline S \,= \,3{U_{\rm{f}}}I_{\rm{f}}^*</latex> | + | <latex>\underline S \,= \,3{U_{\rm{f}}}I_{\rm{f}}^*,</latex> |
njena absolutna vrednost pa je | njena absolutna vrednost pa je | ||
| - | <latex>{S \,= \,3{U_{\rm{f}}}{I_{\rm{f}}}}|||(VA)</latex> | + | <latex>{S \,= \,3{U_{\rm{f}}}{I_{\rm{f}}}}|||(VA).</latex> |
| Vrstica 88: | Vrstica 88: | ||
| - | Če medfazno napetost simetričnega trifaznega sistema na splošno označimo z '''''U''''' in linijski tok z '''''I''''' | + | Če medfazno napetost simetričnega trifaznega sistema na splošno označimo z '''''U''''' in linijski tok z '''''I''''' ter upoštevamo, da je ''U'' = √3 ''U''<sub>f</sub>, fazni tok pa je enak linijskemu, ''I''<sub>f</sub> = ''I'', dobimo še enačbe: |
| - | <latex>{S \,= \,3\frac{U}{\sqrt 3 }I\, = \,\sqrt 3 \,UI}|||(VA) | + | <latex>{S \,= \,3\frac{U}{\sqrt 3 }I\, = \,\sqrt 3 \,UI}|||(VA),</latex> |
| Vrstica 98: | Vrstica 98: | ||
in | in | ||
| - | <latex>{Q\, =\, \sqrt 3 \,UI\,\sin \varphi }|||(var)</latex> | + | <latex>{Q\, =\, \sqrt 3 \,UI\,\sin \varphi }|||(var).</latex> |
Redakcija: 23:06, 8. maj 2010
Ne glede na način obremenitve je navidezna moč trifaznih tokov v kompleksni obliki enaka vsoti kompleksnih navideznih moči posameznih faz.
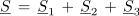
Pri pretežno induktivni simetrični obremenitvi navedeni izraz lahko preide v obliko:
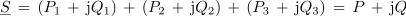
- Delovna moč trifaznih tokov je enaka aritmetični vsoti delovnih moči posameznih faznih tokov.
- Jalova moč trifaznih tokov je enaka aritmetični vsoti jalovih moči posameznih faznih tokov.
- Navidezna moč trifaznih tokov je enaka geometrični vsoti delovne in jalove moči trifaznih tokov.
Moč enofaznega izmeničnega toka je utripajoča. Poglejmo, kako je s časovnim potekom delovne moči v trifaznem simetrično obremenjenem sistemu (sl. a in b).
SLIKA Delovna moč dveh enakih, za 120 ° fazno premaknjenih tokov a) in treh enakih, za 120 ° fazno premaknjenih tokov b)
- Delovna moč trifaznega porabnik v trifaznem sistemu je konstantna, dotok energije porabniku pa enakomeren.
Računanje dela je v takem primeru enostavno:
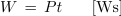
Moč trifaznega sistema s porabniki v zvezdi
V štirivodnem nesimetričnem sistemu se fazni toki generatorja (sistema) med seboj razlikujejo po velikosti in fazi. Navidezno moč sistema izračunamo kot geometrično vsoto navideznih faznih moči:
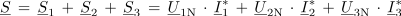
delovno kot aritmetično vsoto delovnih faznih moči
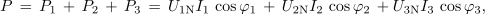
jalovo moč pa pri pretežno induktivni obremenitvi kot aritmetično vsoto jalovih faznih moči:
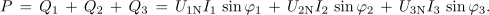
V simetrično obremenjenem sistemu v zvezdi so impedance in fazni toki enaki po velikosti in fazi, zato se računanje moči poenostavi. Če fazno napetost na splošno označimo z Uf, lahko zapišemo:
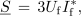
njena absolutna vrednost pa je
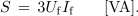
- Navidezna moč simetričnega sistema v zvezdi je enaka trikratni navidezni moči ene faze.
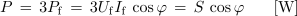
- Delovna moč simetričnega sistema v zvezdi je enaka trikratni delovni moči ene faze.
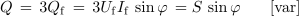
- Jalova moč uravnoteženega sistema v zvezdi je enaka trikratni jalovi moči ene faze.
Če medfazno napetost simetričnega trifaznega sistema na splošno označimo z U in linijski tok z I ter upoštevamo, da je U = √3 Uf, fazni tok pa je enak linijskemu, If = I, dobimo še enačbe:
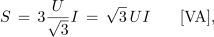
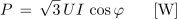
in
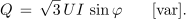
Primer:
Primer:
1. Trifazni izmenični motor s cos φ = 0,83 je v zvezdi priključen na trifazno napetost 400/230 V. Izračunaj moči motorja, če v priključnih vodnikih teče tok 7,9 A!Trifazni motor obremenjuje trifazni sistem simetrično, zato je: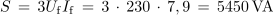
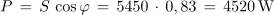
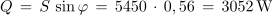
Podpoglavja:
| | 8.3.1 Moč trifaznega sistema s porabniki v zvezdi |
