Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| Vrstica 1: | Vrstica 1: | ||
| - | [[Slika:OET2_a_poglavje_08_slika_01.svg|thumb|Kompleksno število <latex>z</latex> je točka v kompleksni oziroma | + | [[Slika:OET2_a_poglavje_08_slika_01.svg|thumb|Kompleksno število <latex>z</latex> je točka v kompleksni oziroma Gaussovi ravnini štirih kvadrantov.]] |
[[Slika:OET2_a_poglavje_08_slika_02.svg|thumb|Kompleksno število <latex>z</latex> , njemu konjugirano število <latex>z*</latex>, absolutna vrednost <latex>{\mathrm{abs}(z)}</latex> in argument <latex>{\mathrm{arg}(z)}</latex> kompleksnega števila.]] | [[Slika:OET2_a_poglavje_08_slika_02.svg|thumb|Kompleksno število <latex>z</latex> , njemu konjugirano število <latex>z*</latex>, absolutna vrednost <latex>{\mathrm{abs}(z)}</latex> in argument <latex>{\mathrm{arg}(z)}</latex> kompleksnega števila.]] | ||
Vpeljavo števil terjajo računske operacije. Brez celih števil »ni odštevanja« in brez ulomljenih ali racionalnih »ni deljenja«. Po novi razširitvi kliče korenjenje: kvadratni koren pozitivnega števila ni več nujno racionalno, ampak more biti celo iracionalno; racionalna in iracionalna tvorijo realna števila. Za nov »zaplet« poskrbi kvadratni koren (negativnega) števila <latex>-k, k>0</latex>; ni moč najti realnega števila, katerega kvadrat bi bil enak <latex>-k</latex>. Z vpeljavo imaginarne enote <latex>\mathrm{i}</latex> na način, da velja zanjo enačba | Vpeljavo števil terjajo računske operacije. Brez celih števil »ni odštevanja« in brez ulomljenih ali racionalnih »ni deljenja«. Po novi razširitvi kliče korenjenje: kvadratni koren pozitivnega števila ni več nujno racionalno, ampak more biti celo iracionalno; racionalna in iracionalna tvorijo realna števila. Za nov »zaplet« poskrbi kvadratni koren (negativnega) števila <latex>-k, k>0</latex>; ni moč najti realnega števila, katerega kvadrat bi bil enak <latex>-k</latex>. Z vpeljavo imaginarne enote <latex>\mathrm{i}</latex> na način, da velja zanjo enačba | ||
| Vrstica 58: | Vrstica 58: | ||
| - | <latex>{x = {\mathrm {Re} } (z) = \left| z \right|{\mathrm{cos} }\alpha}</latex> in <latex>{y = {\mathrm {Im} } (z) = \left| z \right|\sin \alpha | + | <latex>{x = {\mathrm {Re} } (z) = \left| z \right|{\mathrm{cos} }\alpha}</latex> in <latex>{y = {\mathrm {Im} } (z) = \left| z \right|\sin \alpha .}</latex> |
| Vrstica 76: | Vrstica 76: | ||
| - | + | Ponuja pa se tudi priložnost, da zapišemo število <latex>z</latex> še v ''trigonometrični'' obliki: | |
| Vrstica 91: | Vrstica 91: | ||
| - | '''Zgled 1 | + | '''Zgled 1 ''' |
| - | Dano je kompleksno število: <latex>z = 3 - {\rm{i}}4</latex> (slika 4). Določimo število <latex>z*</latex>, absolutno vrednost in argument | + | Dano je kompleksno število: <latex>z = 3 - {\rm{i}}4</latex> (slika 4). Določimo število <latex>z*</latex>, absolutno vrednost in argument. ⇒ V smislu opredelitev sledijo odgovori: |
Redakcija: 23:41, 19. maj 2010
Slika:OET2 a poglavje 08 slika 01.svg
Kompleksno število  je točka v kompleksni oziroma Gaussovi ravnini štirih kvadrantov.
je točka v kompleksni oziroma Gaussovi ravnini štirih kvadrantov.

Slika:OET2 a poglavje 08 slika 02.svg
Kompleksno število  , njemu konjugirano število
, njemu konjugirano število 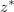 , absolutna vrednost
, absolutna vrednost 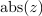 in argument
in argument 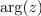 kompleksnega števila.
kompleksnega števila.

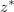
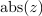
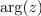
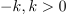
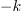
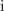
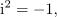
se ponuja nadaljevanje:
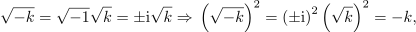
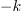
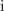

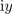
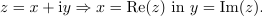

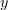


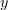

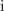

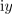
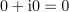

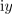
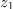
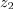
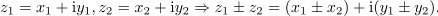
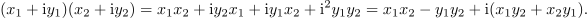

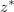

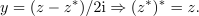
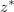
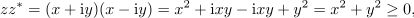

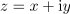
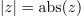
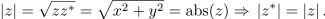

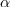
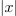
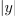

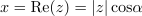
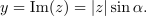
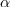


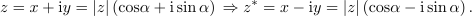
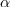
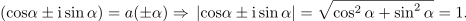
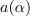
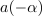
Zgled 1
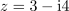
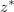
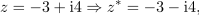
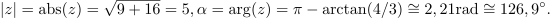
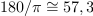
Podpoglavja:
- 1.3.1 Kompleksna količina in kazalec
- 1.3.2 Kazalec harmonične količine
- 1.3.3 Grafično seštevanje (odštevanje) kazalcev
- 1.3.4 »Prehitevanje in zaostajanje kazalcev«
- 1.3.5 Grafično množenje (deljenje) kazalcev
- 1.3.6 Množenje in deljenje z »j«
- 1.3.7 Eulerjeva formula
| | 1.3.1 Kompleksna količina in kazalec |
